How to Design a Mobile Home Roof
The author designed and built this standard house roofing system for an existing mobile home. The design was approved by the framing inspections of the local city's building permit department. The added roof makes heating and cooling the mobile home much more efficient. The noise level inside the home from outside sources like rain storms is greatly reduced. After many years of installation there are no structural problems like leaking, sagging or unevenness. The new roof easily handles the weight of snow, ice and several people walking on it to clean it every year.
How to Design a Mobile Home Roof

-
Determine if the existing mobile home's foundation and structure will withstand the added weight of the roof.
-
Measure the existing mobile home's length and width.
-
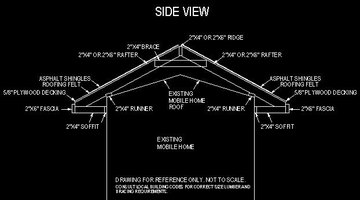
Determine the pitch of the existing mobile home roof. The pitch is the measurement of the slope of the roof. It is usually measured in inches compared to linear feet. For example a 4/12 roof pitch means for every 12 inches of distance the roof will rise 4 inches. Draw a horizontal level line from the highest point on the top of each outside wall. Measure the distance from the center of the line to the top ridge of the roof. For example, if it is 7 feet from the outside wall to the center of the mobile home and it is 21 inches from the center of the level line to the top of the roof ridge, then the existing roof pitch is 3/12. This represents a 3 inch rise for every foot of length.
-
Use the tape measure to determine the pitch of the new mobile home roof. Measure from the top of the proposed ridge location of the new roof to the center of the level line used to determine the existing roof pitch. The new roof must be steep enough to allow for the horizontal braces installed under each pair of rafters. See the side view detail for location for these braces. The steeper the roof the longer the rafters will need to be to allow for the overhanging soffit distance. The new roof's pitch will be used to determine the angle to cut each end of the rafters at the time of installation. The length of the horizontal braces will also be determined by the pitch of the new roof.
-
Create a materials list based on the size of the mobile home and the items needed to construct the new roof and soffit. Include each item shown in the side view and identified below to formulate the materials list. The list should include assorted sizes and lengths of lumber, plywood, assorted nails, roofing felt, asphalt shingles, assorted vent pipes and flanges for each vent. For example, a mobile home that is a single wide 14 ft X 70 ft home with 1 ft of soffit overhang will need 144 linear feet of 2 inch X 4 inch lumber for the runners only. Consult the local building supply store for lengths, types and prices available. Consult local building codes or knowledgeable builders for the determination of the sizes of lumber needed for the rafters and bracing. Rafters should be spaced 16" apart. Local codes may allow 2' spacing but 16" will make a much sturdier and longer lasting roof. The new areas located in the gable ends of the home along with the soffit and fascia can be covered with plywood, vinyl siding or other materials. Use calculator to figure and add these to your materials list. Standard 16 penny coated nails can be used to attach runners, rafters, ridge board, braces and soffit to existing home. Standard 8 penny coated nails can be used for attaching plywood decking to rafters. Standard aluminum roofing nails can be used for attaching roofing felt and shingles to plywood decking. Other approved fasteners can be substituted as codes allow in your area.
-
Count and measure the number of existing plumbing or furnace vents in the existing mobile home roof. These are locations where any pipes are extending through the existing roof. A typical mobile home of this size will have two bathroom vents and one furnace vent. Each vent pipe will need to be extended through the new roof. Use the same materials to extend the vent pipes that they are made of (PVC, aluminum, etc.). Each vent will also need an appropriate flange installed to prevent leaks at each location on the new roof. Flanges are available in many different sizes and types. Check local availability and personal preferences for the types and methods to install. Add these items to your materials list.
-
Add air-circulation vents to your materials list. Several varieties of vents can be used for this. Stationary vents, turbine vents or ridge vents are common. Air vents will also need to be added to the gable ends and soffit area. Air vents that extend the entire length of the mobile home will provide maximum air circulation in the soffit area. Air needs to circulate easily throughout the space between the new and old roof.
References
- Author Ed English
Tips
- Familiarity with carpentry and use of hand tools will greatly aid this project.
- Adding extra insulation between rafters at the time of construction will ease installation and improve the insulating factors and noise reduction of the new roof.
- The soffit overhangs are one foot in length in the picture of the finished mobile home above.
- The mobile home and soffit area were covered with vinyl siding after construction.
Warnings
- Consult local building codes for acceptable building materials and practices used in your region of the country.
- Using the proper size, type and amount of nails in the correct locations are critical for the structural integrity of the new roof.
- Always use proper safety equipment and practices when working on ladders or around construction projects.
Writer Bio
Ed English began his writing career with his first book titled "SCUBA Diving A Newcomer's Point of View" published in 2005. English has owned businesses for over 25 years; he holds several certifications from the National Cable Television Institute, Professional Association of Diving Instructors, American Sailing Association and a Home Inspector Certification.
Photo Credits
- Copyright © 2009 English Explorers LLC
More Articles



