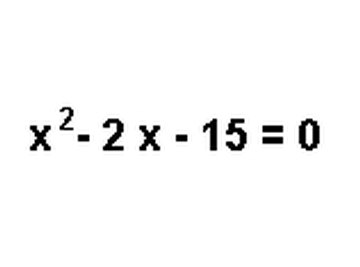
A quadratic trinomial is comprised a quadratic equation and a trinomial expression. A trinomial simply means a polynomial, or more than one term, expression made up of three terms, hence the prefix "tri." Also, no term can be above the second power. A quadratic equation is a polynomial expression equal to zero. Combined, a quadratic trinomial is a three-term equation set to zero. Factoring quadratic trinomials is done just like any other polynomial. One added step is that each factor can be set to zero and solved for x, resulting in more than one possible answer. Use the included images as examples of each step.
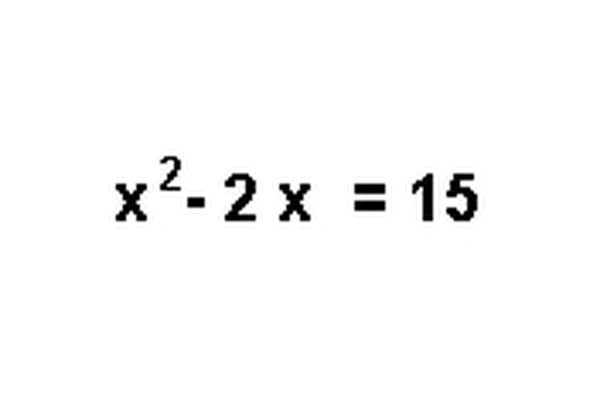
Write the original trinomial equation or expression on paper. You will need to refer back to this item throughout the factoring process.
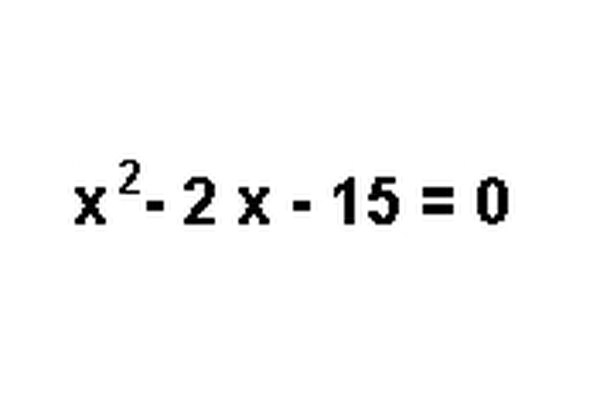
Create a quadratic equation. Group all terms on to the left side of the equation and set it equal to zero on the right side of the equal sign. Simplify the left side, if possible.
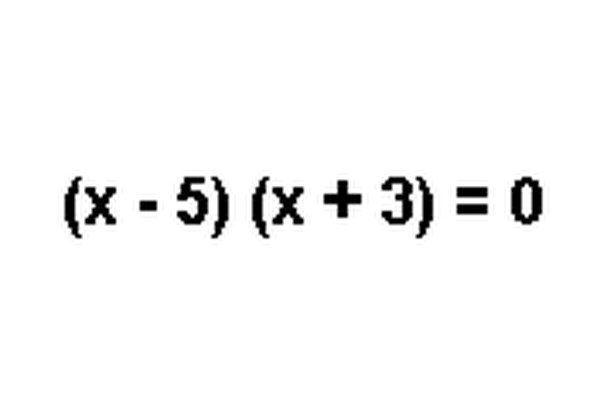
Factor the quadratic equation as you would any other trinomial expression. You need to create two simple factors that, when multiplied, equal the original expression. Keep in mind the order of operations for the factors to equal the trinomial is represented by the acronym, FOIL (First, Outside, Inside, Last terms.) Using FOIL, the product of the two factors needs to equal the expression. The product of the two front terms equals the first term of the trinomial and product of the two last terms equals the last term of the trinomial. The sum of the products of the outer and inner terms must equal the middle term of the trinomial. Basically, you must find two factors whose product equals the last term of the trinomial and whose sum also equals the middle term of the trinomial.
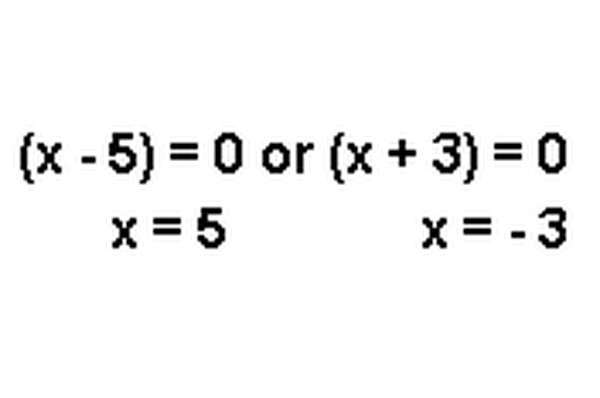
Set each factor equal to zero and solve for x. Each factor is now a linear equation set to zero. Remember the quadratic equations often have more than one possible solution, such that both equations may be correct.
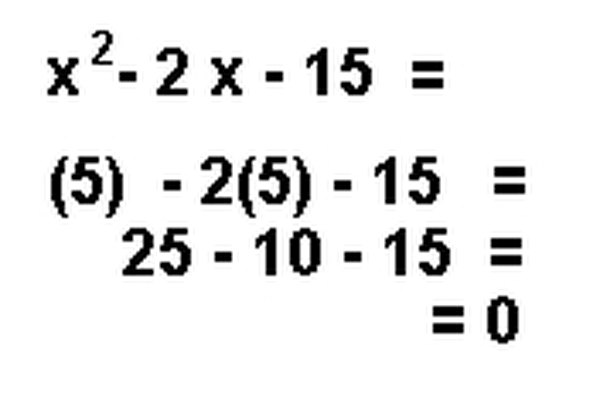
Confirm the solutions from Step 4. Simply plug one of the linear equation solutions back into the original quadratic trinomial equation in place of x and solve to confirm that the entire equation equals zero. Do the same for the other linear equation solution.
About the Author
John Gugie has been a freelance writer for a decade. His work is diverse, from editorials and research papers to entertainment, humor and more. He holds a degree in finance from Moravian College of Pennsylvania. He writes for several sites including Associated Content, Helium and Examiner.
Photo Credits
John Gugie
