The tangent is one of the three basic trigonometric functions, the other two being sine and cosine. These functions are essential to the study of triangles and relate the angles of the triangle to its sides. The simplest definition of the tangent uses the ratios of the sides of a right triangle, and modern methods express this function as the sum of an infinite series. Tangents can be calculated directly when the lengths of the sides of the right triangle are known and can also be derived from other trigonometric functions.
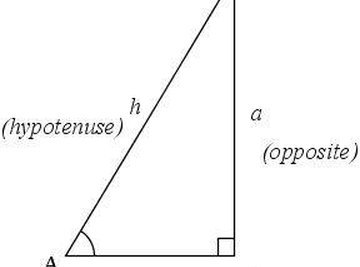
Identify and label the parts of a right triangle. The right angle will be at vertex C, and the side opposite it will be the hypotenuse h. The angle θ will be at vertex A, and the remaining vertex will be B. The side adjacent to angle θ will be side b and the side opposite angle θ will be side a. The two sides of a triangle that are not the hypotenuse are known as the legs of the triangle.
Define the tangent. The tangent of an angle is defined as the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle. In the case of the triangle in Step 1, tan θ = a/b.
Determine the tangent for a simple right triangle. For example, the legs of an isosceles right triangle are equal, so a/b = tan θ = 1. The angles are also equal so θ = 45 degrees. Therefore, tan 45 degrees = 1.
Derive the tangent from the other trigonometric functions. Since sine θ = a/h and cosine θ = b/h, then sine θ / cosine θ = (a/h) / (b/h) = a/b = tan θ. Therefore, tan θ = sine θ / cosine θ.
Calculate the tangent for any angle and desired accuracy:
sin x = x - x^3/3! + x^5/5! - x^7/7! + ... cosine x = 1 - x^2/2! + x^4/4! - x^6/6! + ... So tan x = (x - x^3/3! + x^5/5! - x^7/7! + ...) / (1 - x^2/2! + x^4/4! - x^6/6! + ...)
References
About the Author
Allan Robinson has written numerous articles for various health and fitness sites. Robinson also has 15 years of experience as a software engineer and has extensive accreditation in software engineering. He holds a bachelor's degree with majors in biology and mathematics.
Photo Credits
Wikimedia Commons
