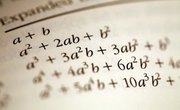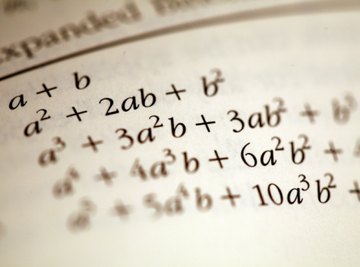
Trinomials are polynomials with exactly three terms. These are usually polynomials of degree two -- the largest exponent is two, but there is nothing in the definition of trinomial that implies this -- or even that the exponents are integers. Fractional exponents make polynomials hard to factor, so typically you make a substitution so the exponents are integers. The reason polynomials are factored is that the factors are much easier to solve than the polynomial -- and the roots of the factors are the same as the roots of the polynomial.
Multiple roots show up on graphs as curves that just touch the X axis at one point.
The mistake that students often make in problems like this is to forget to undo the substitution after the roots of the polynomial have been found.
Make a substitution so the exponents of the polynomial are integers, because the factoring algorithms assume that polynomials are non-negative integers. For example, if the equation is X^1/2 = 3X^1/4 - 2, make the substitution Y = X^1/4 to get Y^2 = 3Y - 2 and put this in standard format Y^2 - 3Y + 2 = 0 as a prelude to factoring. If the factoring algorithm produces Y^2 - 3Y + 2 = (Y -1)(Y - 2) = 0, then the solutions are Y = 1 and Y = 2. Because of the substitution, the real roots are X = 1^4 = 1 and X = 2^ 4 = 16.
Put the polynomial with integers in standard form -- the terms have the exponents in descending order. The candidate factors are made from combinations of factors of the first and last numbers in the polynomial. For example, the first number in 2X^2 - 8X + 6 is 2, which has factors 1 and 2. The last number in 2X^2 - 8X + 6 is 6, which has factors 1, 2, 3 and 6. Candidate factors are X - 1, X + 1, X - 2, X + 2, X - 3, X + 3, X - 6, X + 6, 2X - 1, 2X + 1, 2X - 2, 2X + 2, 2X - 3, 2X + 3, 2X - 6 and 2X + 6.
Find the factors, find the roots and undo the substitution. Try the candidates to see which ones divide the polynomial. For example, 2X^2 - 8X + 6 = (2X -2)(x - 3) so the roots are X = 1 and X = 3. If there was a substitution to make the exponents integers, this is the time to undo the substitution.
Tips
Warnings
References
Tips
- Multiple roots show up on graphs as curves that just touch the X axis at one point.
Warnings
- The mistake that students often make in problems like this is to forget to undo the substitution after the roots of the polynomial have been found.
Photo Credits
Jupiterimages/Photos.com/Getty Images