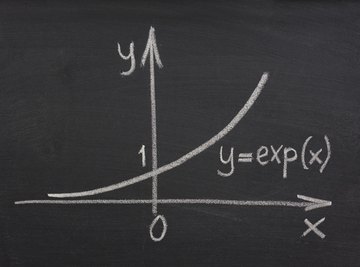
The letter E can have two different meaning in math, depending on whether it's a capital E or a lowercase e. You usually see the capital E on a calculator, where it means to raise the number that comes after it to a power of 10. For example, 1E6 would stand for 1 × 106, or 1 million. Normally, the use of E is reserved for numbers that would be too long to be displayed on the calculator screen if they were written out longhand.
Mathematicians use the lowercase e for a much more interesting purpose – to denote Euler's number. This number, like π, is an irrational number, because it has a non-recurring decimal that stretches to infinity. Like an irrational person, an irrational number seems to make no sense, but the number that e denotes doesn't have to make sense to be useful. In fact, it's one of the most useful numbers in mathematics.
E in Scientific Notation, and the Meaning of 1E6
You don't need a calculator to use E to express a number in scientific notation. You can simply let E stand for the base root of an exponent, but only when the base is 10. You wouldn't use E to stand for base 8, 4 or any other base, especially if the base is Euler's number, e.
When you use E in this way, you write the number xEy, where x is the first set of integers in the number and y is the exponent. For example, you would write the number 1 million as 1E6. In regular scientific notation, this is 1 × 106, or 1 followed by 6 zeros. Similarly 5 million would be 5E6, and 42,732 would be 4.27E4. When writing a number in scientific notation, whether you use E or not, you usually round to two decimal places.
Where Does Euler's Number, e, Come From?
The number represented by e was discovered by mathematician Leonard Euler as a solution to a problem posed by another mathematician, Jacob Bernoulli, 50 years earlier. Bernoulli's problem was a financial one.
Suppose you put $1,000 in a bank that pays 100% annual compound interest and leave it there for a year. You'll have $2,000. Now suppose the interest rate is half that, but the bank pays it twice a year. At the end of a year, you'd have $2,250. Now suppose the bank paid only 8.33%, which is 1/12 of 100%, but paid it 12 times a year. At the end of the year, you'd have $2,613. The general equation for this progression is:
where r is 1 and n is the payment period.
It turns out that, as n approaches infinity, the result gets closer and closer to e, which is 2.7182818284 to 10 decimal places. This is how Euler discovered it. The maximum return you could get on an investment of $1,000 in one year would be $2,718.
Euler's Number in Nature
Exponents with e as a base are known as natural exponents, and here's the reason. If you plot a graph of
you'll get a curve that increases exponentially, just as you would if you plotted the curve with base 10 or any other number. However, the curve y = ex has two special properties. For any value of x, the value of y equals the value of the slope of the graph at that point, and it also equals the area under the curve up to that point. This makes e an especially important number in calculus and in all the areas of science that use calculus.
The logarithmic spiral, which is represented by the equation
is found throughout nature, in seashells, fossils and and flowers. Moreover, e turns up in numerous scientific contexts, including the studies of electric circuits, the laws of heating and cooling, and spring damping. Even though it was discovered 350 years ago, scientists continue to find new examples of Euler's number in nature.
References
About the Author
Chris Deziel holds a Bachelor's degree in physics and a Master's degree in Humanities, He has taught science, math and English at the university level, both in his native Canada and in Japan. He began writing online in 2010, offering information in scientific, cultural and practical topics. His writing covers science, math and home improvement and design, as well as religion and the oriental healing arts.
Photo Credits
Marek Uliasz/iStock/Getty Images
