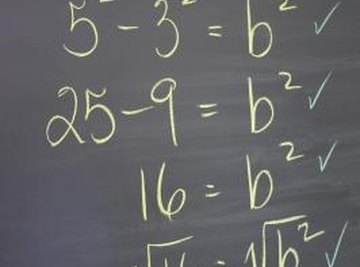
In your Algebra classes, you will need to cultivate a working knowledge of square roots. Square roots are the numbers that, when multiplied by themselves, equal the number under the square root sign. For instance, sqrt(9) equals 3, since 3*3 equals 9. You should memorize the values of square roots, at least up through 100. Once you do that, you will easily be able to determine which perfect square, and subsequently, which square root, is between two integers.
Determine which perfect square is between the two integers. A perfect square is a number of which you can take the square root and obtain two whole numbers. 49 is a perfect square, since it equals 7*7; 56 is not. If you have 35.2 and 37T, 36 is the perfect square between the two integers.
Take the square root of the perfect square. If you have your square roots for memory, you know that the square root of 36 is equal to 6.
Use a calculator to check your work. Take the square root of 36, as well as the square roots of the two integers surrounding 36, and make sure that the square root of 36 is between the square roots of the two integers.
References
About the Author
Tricia Lobo has been writing since 2006. Her biomedical engineering research, "Biocompatible and pH sensitive PLGA encapsulated MnO nanocrystals for molecular and cellular MRI," was accepted in 2010 for publication in the journal "Nanoletters." Lobo earned her Bachelor of Science in biomedical engineering, with distinction, from Yale in 2010.
Photo Credits
Hemera Technologies/AbleStock.com/Getty Images
