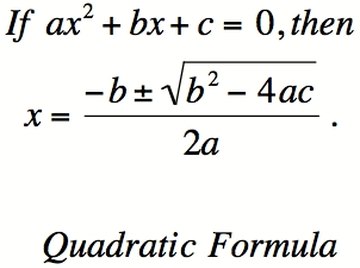
The factoring of a polynomial refers to finding polynomials of lower order (highest exponent is lower) that, multiplied together, produce the polynomial being factored. For example, x^2 - 1 can be factored into x - 1 and x + 1. When these factors are multiplied, the -1x and +1x cancel out, leaving x^2 and 1.
Of Limited Power
Unfortunately, factoring is not a powerful tool, which limits its use in everyday life and technical fields. Polynomials are heavily rigged in grade school so that they can be factored. In everyday life, polynomials are not as friendly and require more sophisticated tools of analysis. A polynomial as simple as x^2 + 1 isn't factorable without using complex numbers--i.e., numbers that include i = √(-1). Polynomials of order as low as 3 can be prohibitively difficult to factor. For example, x^3 - y^3 factors to (x - y)(x^2 + xy + y^2), but it factors no further without resorting to complex numbers.
High School Science
Second-order polynomials--e.g., x^2 + 5x + 4--are regularly factored in algebra classes, around eighth or ninth grade. The purpose of factoring such functions is to then be able to solve equations of polynomials. For example, the solution to x^2 + 5x + 4 = 0 are the roots of x^2 + 5x + 4, namely, -1 and -4. Being able to find the roots of such polynomials is basic to solving problems in science classes in the following 2 to 3 years. Second-order formulas come up regularly in such classes, e.g., in projectile problems and acid-base equilibrium calculations.
The Quadratic Formula
In coming up with better tools to replace factoring, you must recall what the purpose of factoring is in the first place: to solve equations. The quadratic formula is a way of working around the difficulty of factoring some polynomials while still serving the purpose of solving an equation. For equations of second-order polynomials (i.e., of form ax^2 + bx + c), the quadratic formula is used to find the polynomial's roots and therefore the equation's solution. The quadratic formula is x = [-b +/- √(b^2 - 4ac)] / [2a], where +/- means "plus or minus." Notice there is no need to write (x - root1)(x - root2) = 0. Instead of factoring to solve the equation, the solution of the formula can be solved directly without factoring as an intermediary step, though the method is based on factorization.
This is not to say that factoring is dispensable. If students learned the quadratic equation of solving equations of polynomials without learning factoring, understanding of the quadratic equation would be reduced.
Examples

This is not to say that factorization of polynomials is never done outside of algebra, physics and chemistry classes. Handheld financial calculators perform an everyday interest calculation using a formula that is the factorization of future payments with the interest component backed out (see diagram). In differential equations (equations of rates of change), factorization of polynomials of derivatives (rates of change) is performed to solve what are called "homogeneous equations of arbitrary order." Another example is in introductory calculus, in the method of partial fractions to make integration (solving for the area under a curve) easier.
Computational Solutions and the Use of Background Learning
These examples are, of course, far from everyday. And when the factoring gets tough, we have calculators and computers to do the heavy lifting. Instead of expecting a one-to-one match between each mathematical topic taught and everyday calculations, look at the preparation the topic provides for more practical study. Factoring should be appreciated for what it is: a stepping stone to learning methods of solving increasingly realistic equations.
About the Author
Paul Dohrman's academic background is in physics and economics. He has professional experience as an educator, mortgage consultant, and casualty actuary. His interests include development economics, technology-based charities, and angel investing.
